二分图又称作偶图,是图论中的一种特殊模型。
设 G=(V,E) 是一无向图,若顶点 V 可分割为两个互不相交的子集 (A,B),且图中的每条边(i,j)所关联的两个顶点 i 和 j 分属这两个不同的顶点集 (i ∈ A,j ∈ B),则称图 G 为一二分图。
二分图的最大匹配
设G为二分图,若在G的子图M中,任意两条边都没有公共节点,那么称M为二分图G的一组匹配。在二分图中,包含边数最多的一组匹配称为二分图的最大匹配。
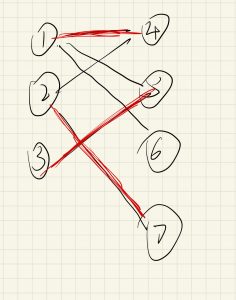
交替路:从一个未匹配点出发,依次经过非匹配边、匹配边、非匹配边…形成的路叫做交替路。
增广路:从一个未匹配点出发,走交替路若能到达另一个未匹配点,则这条交替路称为增广路 。
例如。3->5->1->4->2->7
观察增广路,我们会发现:非匹配边比匹配边多一条。只要把增广路中的匹配边和非匹配边的身份交换(即倒过来走),交换后,图中的匹配边数目比原来多了1条。
这里的增广路就是指能增加匹配边的一条路。

设绿色表示匹配边。左图3为非匹配点,右图经过匹配边和非匹配边的身份交换,从匹配点7开始走。
匈牙利算法:通过不停地找增广路来增加匹配边。找不到增广路时,达到最大匹配。可以用DFS或BFS来实现。
2063 过山车
Problem Description
RPG girls今天和大家一起去游乐场玩,终于可以坐上梦寐以求的过山车了。可是,过山车的每一排只有两个座位,而且还有条不成文的规矩,就是每个女生必须找个个男生做partner和她同坐。但是,每个女孩都有各自的想法,举个例子把,Rabbit只愿意和XHD或PQK做partner,Grass只愿意和linle或LL做partner,PrincessSnow愿意和水域浪子或伪酷儿做partner。考虑到经费问题,boss刘决定只让找到partner的人去坐过山车,其他的人,嘿嘿,就站在下面看着吧。聪明的Acmer,你可以帮忙算算最多有多少对组合可以坐上过山车吗?
Input
输入数据的第一行是三个整数K , M , N,分别表示可能的组合数目,女生的人数,男生的人数。0<K<=1000
1<=N 和M<=500.接下来的K行,每行有两个数,分别表示女生Ai愿意和男生Bj做partner。最后一个0结束输入。
Output
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
int edge[510][510];//邻接矩阵
bool vis[510];//男生是否已被分配
int match[510];//与男生配对的女生
int K;//可能的组合数目
int M;//女生人数
int N;//男生人数
bool Hungary(int u) {//匈牙利算法
for (int v = 1; v <= N; v++) {//枚举男
if (!vis[v] && edge[u][v] == 1) {
//此轮中男生已被标记,则跳过
vis[v] = 1;//先标记
if (match[v] == 0 || Hungary(match[v])) {//如果此男生还没有配对的女生,或者此男生配对的女生可以让出此男生
match[v] = u;
return true;//配对成功
}
}
}
return false;//配对失败
}
int main() {
int ans;//记录匹配对数
while (cin >> K) {
if (K == 0)break;
cin >> M;
cin >> N;
memset(edge, 0, sizeof(edge));
memset(match, 0, sizeof(match));
int a, b;
for (int i = 0; i < K; i++) {
cin >> a;
cin >> b;
edge[a][b] = 1;
}
ans = 0;
for (int i = 1; i <= M; i++) {//枚举女
memset(vis, 0, sizeof(vis));
if (Hungary(i))ans++;//i能匹配到则++,i匹配不到,则落单
}
cout << ans << endl;
}
}

最新评论