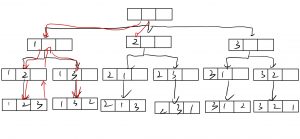
全排列（DFS）

（排列树）

（原题：P1706 全排列问题 – 洛谷 | 计算机科学教育新生态 (luogu.com.cn)）

题目描述

按照字典序输出自然数 11 到 n 所有不重复的排列，即 n 的全排列，要求所产生的任一数字序列中不允许出现重复的数字。

输入格式

一个整数 n。

输出格式

由 1∼n 组成的所有不重复的数字序列，每行一个序列。

每个数字保留 5 个场宽。

输入输出样例

输入 #1

3

输出 #1

1     2     3

1     3     2

2      1     3

2     3     1

3     1     2

3     2     1

#include <iostream>
#include <string>
#include <algorithm>
#include<math.h>
#include<queue>
#include<vector>
using namespace std;

int n;
int visit[10];//标记某整数是否被访问
int ans[10];//输出

void dfs(int step) {
    if (step == n + 1) {//递归出口，第n+1步输出排列
        for (int i = 1; i <= n; i++) {
            printf("%5d", ans[i]);
        }
        cout << endl;
        return;
    }
    for (int i = 1; i <= n; i++) {//此for循环用来寻找未被访问过的数 
        if (visit[i] == 0) {//如果i序列中 
            visit[i] = 1;//则此次递归将该数加入序列 
            ans[step] = i; 
            dfs(step + 1);//递归序列的下一位 
            visit[i] = 0;//还原状态 
        } 
    } 
} 
int main() { 
    cin >> n;
    dfs(1);
}

八皇后问题(回溯)

（原题：P1219 [USACO1.5] 八皇后 Checker Challenge – 洛谷 | 计算机科学教育新生态 (luogu.com.cn)）

题目描述

一个如下的 6×6的跳棋棋盘，有六个棋子被放置在棋盘上，使得每行、每列有且只有一个，每条对角线（包括两条主对角线的所有平行线）上至多有一个棋子。

上面的布局可以用序列 2 4 6 1 3 5来描述，第 i 个数字表示在第 i 行的相应位置有一个棋子，如下：

行号 1 2 3 4 5 6

列号 2 4 6 1 3 5

这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出，解按字典顺序排列。
请输出前 3 个解。最后一行是解的总个数。

输入格式

一行一个正整数 n，表示棋盘是 n×n 大小的。

输出格式

前三行为前三个解，每个解的两个数字之间用一个空格隔开。第四行只有一个数字，表示解的总数。

输入输出样例

输入 #1

6

输出 #1

2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4

#include <iostream>
#include <string>
#include <algorithm>
#include<math.h>
#include<queue>
#include<vector>
using namespace std;

int n;
int hang[15];
int lie[15];
int zhengxie[30];
int nixie[30];
int ans[15];//输出
int ans_num = 0;

void dfs(int step) {//step==行
    if (step == n + 1) {
        ans_num++;
        for (int i = 1; i <= n; i++) {
            cout << ans[i]<<" ";//每一行，输出其列
       }
    cout << endl;
    }

    for (int j = 1; j <= n; j++) {//每列每列的放置 
        if (!(lie[j] || zhengxie[j - step+n] || nixie[j + step])) { //可以放置 
            ans[step] = j; 
            lie[j] = 1; 
            zhengxie[j - step+n] = 1; 
            nixie[j + step] = 1; 

            dfs(step + 1); 

            lie[j] = 0; 
            zhengxie[j - step+n] = 0; 
            nixie[j + step] = 0; 
        } 
    } 
} 
int main() { 
    cin >> n;
    dfs(1);
    cout << ans_num;
}

void dfs(int step) {
    if (到达目的地) {
        输出解
        返回
    }
    剪枝（可选）
    for (int i = 1; i <= 枚举数; i++) {
        if (满足条件) { 
            更新状态
            dfs(step + 1);
            恢复状态
        }
    }
}