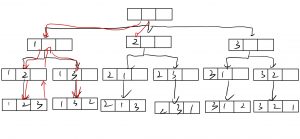
Suppose that all the keys in a binary tree are distinct positive integers. Given the postorder and inorder traversal sequences, you are supposed to output the level order traversal sequence of the corresponding binary tree.

Input Specification:

Each input file contains one test case. For each case, the first line gives a positive integer $N$ ($\le 30$), the total number of nodes in the binary tree. The second line gives the postorder sequence and the third line gives the inorder sequence. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print in one line the level order traversal sequence of the corresponding binary tree. All the numbers in a line must be separated by exactly one space, and there must be no extra space at the end of the line.

Sample Input:

7
2 3 1 5 7 6 4
1 2 3 4 5 6 7

Sample Output:

4 1 6 3 5 7 2

#include<iostream>
#include<queue>

using namespace std;

typedef struct Node {
	int key;
	struct Node* left = NULL;
	struct Node* right = NULL;
}node,*L;//node为节点，*L为指向根的指针

int N;//节点数量
int post[35];//后续
int in[35];//中序
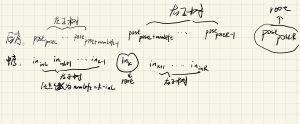
void build_tree(L &root,int post_L,int post_R ,int in_L,int in_R) {//后序序列区间[post_L,post_R]，中序序列区间[in_L,in_R]
	if (post_R < post_L)return; node* temp = new node; temp->key = post[post_R];
	root = temp;
	int index;//根节点在中序中的位置
	for (index = in_L; index <= in_R; index++) { if (in[index] == post[post_R])break; } build_tree(root->left, post_L, index - in_L + post_L - 1, in_L, index - 1);
	build_tree(root->right, index - in_L + post_L, post_R - 1, index + 1, in_R);
}

void BFS(L root) {
	queue<node*> n;
	n.push(root);
	int num = 0;
	while (!n.empty()) {
		node* temp = new node;
		temp = n.front();
		n.pop();
		num++;
		if (num < N) {
			cout << temp->key << ' ';
		}
		else cout << temp->key;
		if (temp->left != NULL)n.push(temp->left);
		if (temp->right != NULL)n.push(temp->right);
	}
}
int main() {
	cin >> N;
	for (int i = 1; i <= N; i++) { cin >> post[i];
	}
	for (int i = 1; i <= N; i++) { cin >> in[i];
	}
	L root = new node;//创建根节点
	//root->key = post[N];
	build_tree(root, 1, N, 1, N);
	//preorder(root);
	BFS(root);
}